The interstitium of a body tissue, which is the space outside blood vessels and cells, contains fibers
Question:
The interstitium of a body tissue, which is the space outside blood vessels and cells, contains fibers of collagen, glycosaminoglycans, and other biopolymers that are surrounded by water. Fluid movement in that space affects the distribution of nutrients and drugs. As in other porous materials, flow in the interstitium can be described using Darcy's law. The model outlined here is a simplified version of one in Baxter and Jain (1989), which was used to explore the therapeutic consequences of interstitial pressure and velocity distributions in “solid” tumors.
Figure P8.13(a) depicts a spherical tumor of radius R that is large enough to contain many blood vessels. The enlarged volume element in Fig. P8.13(b) shows a few blood capillaries and the associated interstitium. In general, there is net flow out of the capillaries. Neglecting the drainage that might occur in lymphatic vessels, the fluid leaving the capillaries must move to the periphery of the tumor via interstitial flow.

(a) Let W be the volume of water moving from the capillaries to the interstitium per unit time, per unit volume of tumor (units of s–1). Assuming that the flow is steady and purely radial, use a balance on a spherical shell of thickness Δr to derive the differential equation that relates W to vr(r). Combine that result (a kind of continuity equation) with Darcy's law to show that
This is the spherical form of Eq. (8.3-46), but with an added source term.
(b) If W is constant, determine![]()
and vr(r). Assume that the Darcy permeability of the interstitium (k) is known and that![]()
(c) Because flow across the permeable wall of a capillary is caused by a pressure difference, a more realistic assumption is that W increases as ℘ decreases. Assume that
where α is the hydraulic permeability of the capillary walls times the capillary surface area per volume of tumor, and![]()
is a constant determined by the intracapillary pressure and the osmotic pressure of dissolved proteins. Again determine![]()
and vr(r).
The differential equation
where m is a real constant, has the general solution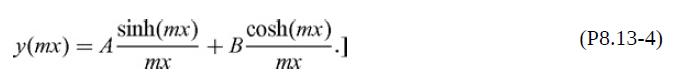
Step by Step Answer:

Introduction To Chemical Engineering Fluid Mechanics
ISBN: 9781107123779
1st Edition
Authors: William M. Deen





