Section 4.1.3 assumes that investment opportunities generate a constant rate of growth of profits in perpetuity. What
Question:
Section 4.1.3 assumes that investment opportunities generate a constant rate of growth of profits in perpetuity. What if the investment opportunities are not available in perpetuity but only over some finite interval of \(T\) periods? What can be said about the relationship between \(r\) and \(k r^{*}\) in both cases?
Data From Section 4.1.3:-
That the approach to evaluating a firm using the stream of earnings is independent of any assumption on the time shape of the dividend stream. However, both streams are somehow indirectly related, since they give rise to the same valuation formula for the firm.
In this section, the preceding evaluation formulas are adapted to illustrate how close the time shapes of the streams of dividends and value are. In order to do that, a specific constraint will be imposed on the stream of earnings, and from the equivalence of the valuation using dividends and earnings, the effect on the stream of dividends will be discussed.
Suppose that the investment schedule \(I_{t}\) is related to the net profit \(X_{t}\) through the relationship
\[I_{t}=k_{i} X_{t}\]
that is, the investments are a constant fraction \(k_{i}\) of the earnings, and such investment provides a constant yield \(r^{*}\) per period. Then the value of \(X_{t}\) is
\[X_{t}=X_{t-1}+r^{*} I_{t-1}=X_{t-1}\left[1+k_{i} r^{*}\right]\]
so that \(X_{t}\) grows at a rate \(k r^{*}\) per period. This means that
\[X_{t+\tau}=X_{t}\left[1+k_{i} r^{*}\right]^{\tau}\]
Assuming that \(k r^{*} To begin with, notice that by definition of \(g\) one has \[d_{t+\tau}=d_{t}[1+g]^{\tau}\] Let \(k_{d}\) be the fraction of the earnings retained in each period, such that the dividends paid are \(D_{t}=X_{t}\left(1-k_{d}\right)\). Note that, \(k_{i}\) being the fraction of the total earnings represented by the investment, the amount of external funds raised at any time \(t\) will be \[\left(k_{i}-k_{d}\right) X_{t}\] Assuming that \(g \[p_{i}=\sum_{\tau=1}^{\infty} \frac{d_{i+\tau}}{(1+r)^{\tau}}=\frac{d_{i+1}}{r-g}\] which is known as the Gordon model for the share price. Recalling that \(D_{i+1}=n_{t} d_{t+1}\) and writing \(V_{t}=n_{t} p_{t}\), one obtains \[V_{i}=\frac{D_{t+1}}{r-g}=\frac{X_{t+1}\left(1-k_{d}\right)}{r-g}\] Equating this expression for \(V_{t}\) with equation (4.8), it follows that \[g=r-\left(\frac{1-k_{d}}{1-k_{i}}\right)\left(r-k_{i} r^{*}\right)\] Notice that, in the particular case of a firm that raises no external funds and is entirely financed with its earnings, it follows that \(k_{i}=k_{d}\) and \(g=k_{i} r^{*}\). In other words, the dividends grow at the same rate as do the net profits and as does the value of the firm.
and therefore the value of the firm grows at the same rate as do the net profits. But it was discussed in the previous section that the valuation of the firm could just as equally be made in terms of the stream of dividends. The question is determining the effective rate of growth of the dividends \(g\) imposed by the constraint that the value of the firm is given by the preceding expression.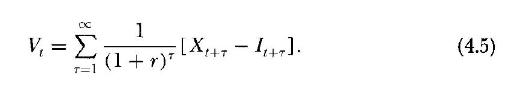
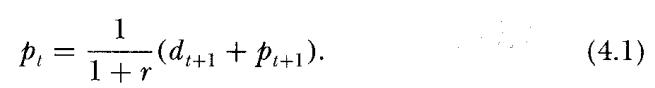
Step by Step Answer:






