This exercise illustrates the case of Lemma 5.2.1 in the model of Diamond (1991). Take (L=R=1, pi=frac{1}{2},
Question:
This exercise illustrates the case of Lemma 5.2.1 in the model of Diamond (1991). Take \(L=R=1, \pi=\frac{1}{2}, X=1 \frac{3}{4}, C=0, f=\frac{1}{2}\), and \(f^{d}=\frac{1}{3}\).
(a) What are the face values of a short-term and a long-term debt contract?
(b) Show that in this example there will be no liquidation.
(c) What is the payoff of a good project financed with long-term debt?
(d) What is the probability that a good project receives a downgrade at \(t=1\) ?
(e) What is the payoff of a good project financed with short-term debt?
Data From Lemma 5.2.1:-
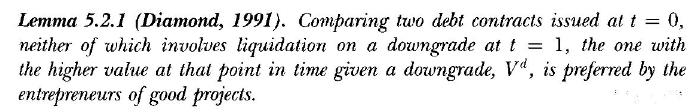
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





