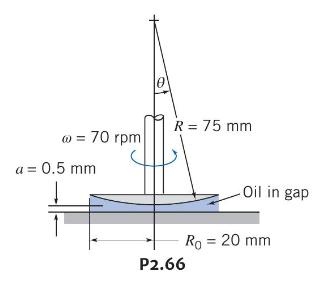
A cross section of a rotating bearing is shown. The spherical member rotates with angular speed \(\omega\), a small distance, \(a\), above the plane surface. The narrow gap is filled with viscous oil, having \(\mu=1250 \mathrm{cp}\). Obtain an algebraic expression for the shear stress acting on the spherical member. Evaluate the maximum shear stress that acts on the spherical member for the conditions shown. (Is the maximum necessarily located at the maximum radius?) Develop an algebraic expression (in the form of an integral) for the total viscous shear torque that acts on the spherical member. Calculate the torque using the dimensions shown.

Transcribed Image Text:

R = 75 mm w = 70 rpm a = 0.5 mm P2.66 Oil in gap Ro = 20 mm