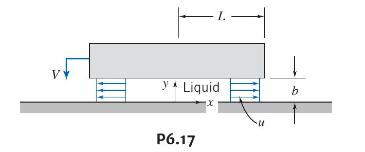
A liquid layer separates two plane surfaces as shown. The lower surface is stationary; the upper surface moves downward at constant speed \(V\). The moving surface has width \(w\), perpendicular to the plane of the diagram, and \(w \gg L\). The incompressible liquid layer, of density \(ho\), is squeezed from between the surfaces. Assume the flow is uniform at any cross section and neglect viscosity as a first approximation. Use a suitably chosen control volume to show that \(u=V x / b\) within the gap, where \(b=b_{0}-V t\). Obtain an algebraic expression for the acceleration of a fluid particle located at \(x\). Determine the pressure gradient, \(\partial p / \partial x\), in the liquid layer. Find the pressure distribution, \(p(x)\). Obtain an expression for the net pressure force that acts on the upper (moving) flat surface.

Transcribed Image Text:

1. y Liquid x b P6.17