A tank contains water (left(20^{circ} mathrm{C} ight)) at an initial depth (y_{0}=1 mathrm{~m}). The tank diameter is

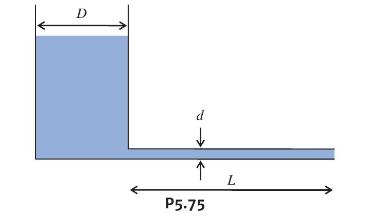
A tank contains water \(\left(20^{\circ} \mathrm{C}\right)\) at an initial depth \(y_{0}=1 \mathrm{~m}\). The tank diameter is \(D=250 \mathrm{~mm}\) and a tube of diameter \(d=3 \mathrm{~mm}\) and length \(L=4 \mathrm{~m}\) is attached to the bottom of the tank. For laminar flow a reasonable model for the water level over time is

\[\frac{d y}{d t}=-\frac{d^{4} ho g}{32 D^{2} \mu L} y \quad y(0)=y_{0}\]

Using Euler methods with time steps of \(12 \mathrm{~min}\) and \(6 \mathrm{~min}\) :

(a) Estimate the water depth after \(120 \mathrm{~min}\), and compute the errors compared to the exact solution

\[y_{\text {exact }}(t)=y_{0} e^{-\frac{d^{4} ho g}{32 D^{2} \mu L} t}\]

(b) Plot the Euler and exact results.

Transcribed Image Text:

D P P5.75 L