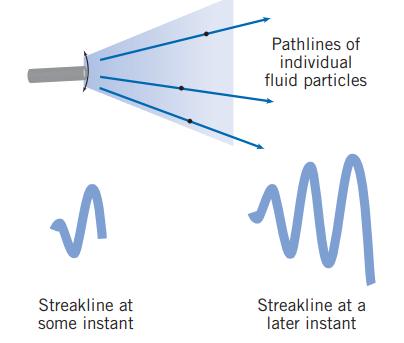
Consider the garden hose of Fig. 2.5. Suppose the velocity field is given by \(\vec{V}=u_{0} \hat{i}+v_{0} \sin \left[\omega\left(t-x / u_{0}\right)\right] \hat{j}\), where the \(x\) direction is horizontal and the origin is at the mean position of the hose, \(u_{0}=10 \mathrm{~m} / \mathrm{s}\), \(v_{0}=2 \mathrm{~m} / \mathrm{s}\), and \(\omega=5 \mathrm{cycle} / \mathrm{s}\). Find and plot on one graph the instantaneous streamlines that pass through the origin at \(t=0 \mathrm{~s}, 0.05 \mathrm{~s}\), \(0.1 \mathrm{~s}\), and \(0.15 \mathrm{~s}\). Also find and plot on one graph the pathlines of particles that left the origin at the same four times.

Data From Fig.2.5

Transcribed Image Text:

T Pathlines of individual fluid particles Streakline at some instant M Streakline at a later instant