For pressure-driven, steady, fully developed laminar flow of an incompressible fluid through a straight channel of length \(L\), we can define the hydraulic resistance as \(R_{\text {hyd }}=\Delta p / Q\), where \(\Delta p\) is the pressure drop and \(Q\) is the flow rate (analogous to the electrical resistance \(R_{\text {elec }}=\Delta V / I\), where \(\Delta V\) is the electrical potential drop and \(I\) is the electric current). The following table summarizes the hydraulic resistance of channels with different cross sectional shapes [30]:

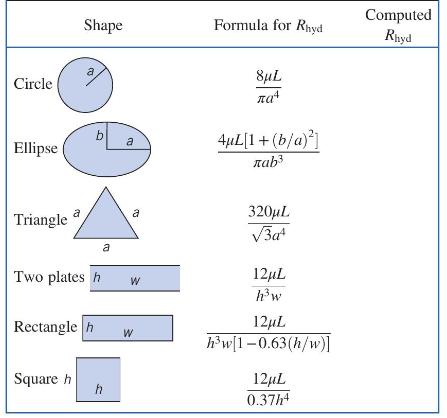
Calculate the hydraulic resistance of a straight channel with the listed cross-sectional shapes using the following parameters for water flow: \(\mu=1 \mathrm{mPa} \cdot \mathrm{s}, L=10 \mathrm{~mm}, a=100 \mu \mathrm{m}, b=33 \mu \mathrm{m}, h=\) \(100 \mu \mathrm{m}\), and \(w=300 \mu \mathrm{m}\). Based on the calculated hydraulic resistance, which shape is the most energy efficient to pump water?

Transcribed Image Text:

Shape Formula for Rhyd Computed Rhyd Circle a Ellipse Triangle b B a a a Two plates h Rectangle h W Square h h 8L 4uL[1+(b/a)2] 320L 3a 12L W hw 12L hw[1 0.63(h/w)] 12L 0.37h4