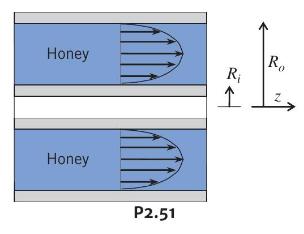
In a food-processing plant, honey is pumped through an annular tube. The tube is \(L=2 \mathrm{~m}\) long, with inner and outer radii of \(R_{i}=5 \mathrm{~mm}\) and \(R_{o}=25 \mathrm{~mm}\), respectively. The applied pressure difference is \(\Delta p=125 \mathrm{kPa}\), and the honey viscosity is \(\mu=5 \mathrm{~N} \cdot \mathrm{s} / \mathrm{m}^{2}\). The theoretical velocity profile for laminar flow through an annulus is:

\[u_{z}(r)=\frac{1}{4 \mu}\left(\frac{\Delta p}{L}\right)\left[R_{i}^{2}-r^{2}-\frac{R_{o}^{2}-R_{i}^{2}}{\ln \left(\frac{R_{i}}{R_{o}}\right)} \cdot \ln \left(\frac{r}{R_{i}}\right)\right]\]

Show that the no-slip condition is satisfied by this expression. Find the location at which the shear stress is zero. Find the viscous forces acting on the inner and outer surfaces, and compare these to the force \(\Delta p \pi\left(R_{o}^{2}-R_{i}^{2}\right)\). Explain.

Transcribed Image Text:

Honey R Ro Z Honey P2.51