The Colebrook equation (Eq. 8.37) for computing the turbulent friction factor is implicit in (f). An explicit
Question:
The Colebrook equation (Eq. 8.37) for computing the turbulent friction factor is implicit in \(f\). An explicit expression [31] that gives reasonable accuracy is
\[f_{0}=0.25\left[\log \left(\frac{e / D}{3.7}+\frac{5.74}{R e^{0.9}}\right)\right]^{-2}\]
Compare the accuracy of this expression for \(f\) with Eq. 8.37 by computing the percentage discrepancy as a function of \(\operatorname{Re}\) and \(e / D\), for \(R e=10^{4}\) to \(10^{8}\), and \(e / D=0,0.0001,0.001,0.01\), and 0.05. What is the maximum discrepancy for these \(\operatorname{Re}\) and \(e / D\) values? Plot \(f\) against \(R e\) with \(e / D\) as a parameter.
Data From (Eq. 8.37)
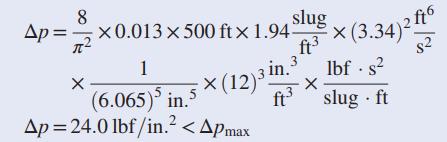
Step by Step Answer:
Related Book For 

Fox And McDonald's Introduction To Fluid Mechanics
ISBN: 9781118912652
9th Edition
Authors: Philip J. Pritchard, John W. Mitchell
Question Posted:




