The velocity field for a plane source located distance (h=1 mathrm{~m}) above an infinite wall aligned along
Question:
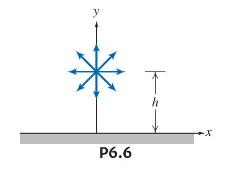
The velocity field for a plane source located distance \(h=1 \mathrm{~m}\) above an infinite wall aligned along the \(x\) axis is given by
\[\begin{aligned} \vec{V}= & \frac{q}{2 \pi\left[x^{2}+(y-h)^{2}\right]}[x \hat{i}+(y-h) \hat{j}] \\ & +\frac{q}{2 \pi\left[x^{2}+(y+h)^{2}\right]}[x \hat{i}+(y+h) \hat{j}] \end{aligned}\]
where \(q=2 \mathrm{~m}^{3} / \mathrm{s} / \mathrm{m}\). The fluid density is \(1000 \mathrm{~kg} / \mathrm{m}^{3}\) and body forces are negligible. Derive expressions for the velocity and acceleration of a fluid particle that moves along the wall, and plot from \(x=0\) to \(x=+10 h\). Verify that the velocity and acceleration normal to the wall are zero. Plot the pressure gradient \(\partial p / \partial x\) along the wall. Is the pressure gradient along the wall adverse (does it oppose fluid motion) or not?
Step by Step Answer:

Fox And McDonald's Introduction To Fluid Mechanics
ISBN: 9781118912652
9th Edition
Authors: Philip J. Pritchard, John W. Mitchell




