A water theme park plays seven games depending on the demand during weekdays and weekends. The park

Question:

A water theme park plays seven games depending on the demand during weekdays and weekends. The park earns revenues (in thousands of euros) from playing these games and the revenue varies with the days. Certain games generate more revenue during weekends and certain games do not yield any revenue. The park analyzed its revenue data and prepared a revenue matrix as follows (values in euros):

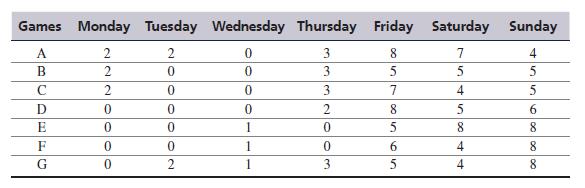
Besides, the machines used for these games require maintenance and have other costs associated with them. The park realizes the games F and G can be played at most 2 times a week; while all other games can be played up to three times a week. On any given day, a game cannot be played more than once. The park also plans to play a maximum of 2 games daily from Monday through Thursday to amuse the few visitors during weekdays. During the weekend (Friday, Saturday, and Sunday), to amuse the large number of visitors, the park plays a maximum of 5 games. The park wants to know which game should be played on which days to maximize revenue.

a. Formulate a linear programming model for this problem.
b. Solve this model using computer.
c. If the park plans to play all seven games during weekends, what will be its revenue?
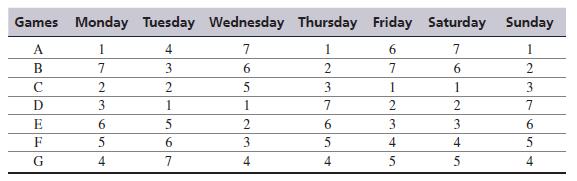
d. If the park considers customers’ ranking (analogously called weights) of games instead of costs and maximizes the ranking while satisfying constraints, how does the solution change? In a study conducted over a week, customers ranked the games as follows. (1: the least liked; 7: the most liked)