13.26 Advertising and Sales A department store conducted an experiment to investigate the effects of advertising expenditures on the weekly sales for its men's wear, children's wear, and women's wear departments. Five weeks for observation were randomly selected from each department, and an advertising budget x, (in hundreds of dollars) was assigned for each. The weekly sales (in thousands of dollars) are shown in the accompanying table for each of the 15 one-week sales periods. If we expect weekly sales E(Y) to be linearly related to advertising expendi- ture x1, and if we expect the slopes of the lines corre- sponding to the three departments to differ, then an appropriate model for E(Y) is

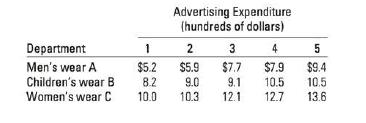
a. Find the equation of the line relating E(Y) to advertising expenditure x, for the men's wear department A. (HINT: According to the coding used for the dummy variables, the model represents mean sales E(Y) for the men's wear department A when x2=x3 = 0. Substitute x2 x3 = 0 into the equa- tion for E(Y) to find the equation of this line.)

b. Find the equation of the line relating E(Y) to x for the children's wear department B. (HINT: According to the coding, the model represents E(Y) for the children's wear department when x2 = 1 and x3 0.)

c. Find the equation of the line relating E(Y) to x for the women's wear department C.

d. Find the difference between the intercepts of the E(Y) lines corresponding to the children's wear B and men's wear A departments.

e. Find the difference in slopes between E(Y) lines corresponding to the women's wear C and men's wear A departments.

f. Refer to part

e. Suppose you want to test the null hypothesis that the slopes of the lines corresponding to the three departments are equal. Express this as a test of hypothesis about one or more of the model parameters.

Transcribed Image Text:

E(Y) = Bo+ + B2x2 + B3x3 + Bxx + xx quantitative dummy variables interaction terms that variable "advertising used to introduce introduce differences the qualitative in slopes expenditure" variable "department" into the model where x Advertising expenditure x2= 1 if children's wear department B lo if not 1 if women's wear department C X30 if not