A bowl contains a blue and b yellow chips. From the bowl, we select successively and without replacement, until the nth blue chip is selected. Let X be the number of chips selected until this happens. The distribution of X is called a negative hypergeometric distribution.

(i) Prove that the probability function of X is given by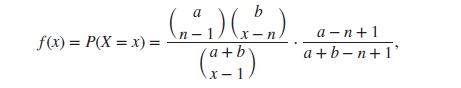

where x = n, n + 1,…, n + b.
(ii) Arguing as in the proof of Proposition 5.9, show that, as a → ∞, b → ∞ in a way such that

the following holds true:

(convergence of the negative hypergeometric distribution to the negative binomial). How do you interpret the last result intuitively?

Application: We have 25 male and 35 female students and we want to select a committee that has exactly 3 female members. For this reason, we select students at random (among the 60 students) and we stop when the third female student is selected. Let X be the number of committee members. Write down the probability function of X. Hence, calculate the expected number of committee members.

Transcribed Image Text:

f(x) = P(X = x)= a (n-1) (xon) (a+b) x- a-n+1 a+b-n+1'