(a) Evaluating the necessary integrals, verify the identities [mu_{2}=alpha+beta mu_{1} quad text { and } quad sigma_{2}^{2}=sigma^{2}+beta^{2}...
Question:
(a) Evaluating the necessary integrals, verify the identities
\[\mu_{2}=\alpha+\beta \mu_{1} \quad \text { and } \quad \sigma_{2}^{2}=\sigma^{2}+\beta^{2} \sigma_{1}^{2}\]
on page 374 .
(b) Substitute \(\mu_{2}=\alpha+\beta \mu_{1}\) and \(\sigma_{2}^{2}=\sigma^{2}+\beta^{2} \sigma_{1}^{2}\) into the formula for the bivariate density given on page 374 , and show that this gives the final form shown on page 375 .
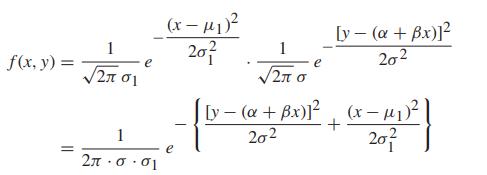
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Probability And Statistics For Engineers
ISBN: 9780134435688
9th Global Edition
Authors: Richard Johnson, Irwin Miller, John Freund
Question Posted:





