A pair of random variables has the circular normal distribution if their joint density is given by

\[\begin{aligned}& f\left(x_{1}, x_{2}\right) \\& \quad=\frac{1}{2 \pi \sigma^{2}} e^{-\left[\left(x_{1}-\mu_{1}\right)^{2}+\left(x_{2}-\mu_{2}\right)^{2}\right] / 2 \sigma^{2}} \\& \text { for }-\infty

(a) If \(\mu_{1}=2\) and \(\mu_{2}=-2\), and \(\sigma=10\), use Table 3 to find the probability that \(-8

(b) If \(\mu_{1}=\mu_{2}=0\) and \(\sigma=3\), find the probability that \(\left(X_{1}, X_{2}\right)\) is contained in the region between the two circles \(x_{1}^{2}+x_{2}^{2}=9\) and \(x_{1}^{2}+x_{2}^{2}=36\).

Data From Table 3

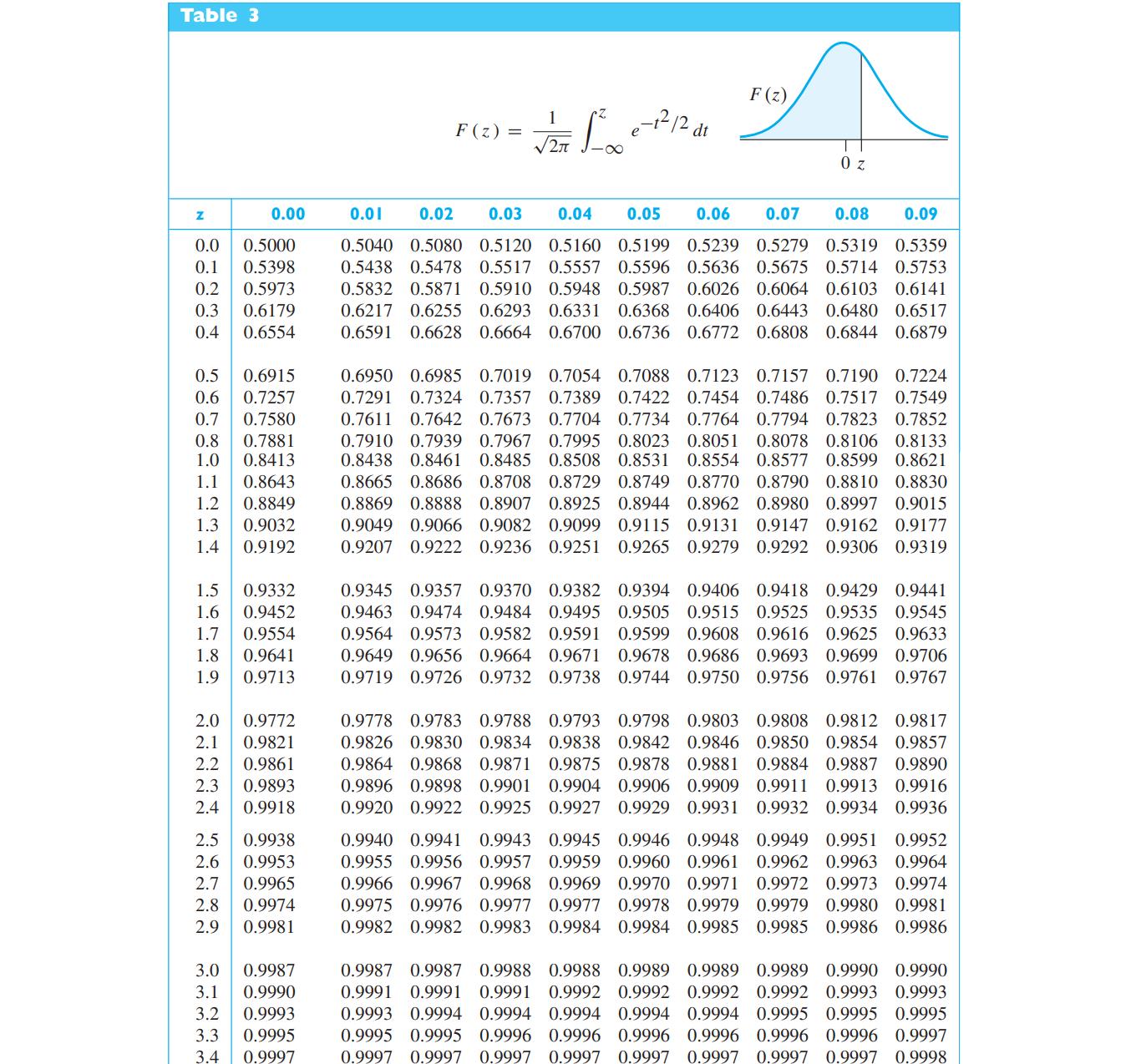
Transcribed Image Text:

Table 3 Z F(z) = 1 2 -12 12 dt F(z) 0 z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.0 0.5000 0.1 0.5398 0.2 0.5973 0.3 0.6179 0.4 0.6554 0.5 0.6915 0.6 0.7257 0.7 0.7580 0.8 0.7881 1.0 0.8413 1.1 0.8643 0.8849 0.9032 0.9192 1.2 1.3 1.4 1.5 0.9332 1.6 0.9452 1.7 0.9554 1.8 0.9641 1.9 0.9713 2.0 0.9772 2.1 0.9821 2.2 0.9861 123 2.3 0.9893 2.4 0.9918 2.5 0.9938 2.6 0.9953 2.7 0.9965 619 2.8 0.9974 2.9 0.9981 3.0 0.9987 0.9990 71 3.1 3.2 0.9993 3.3 0.9995 3.4 0.9997 0.5040 0.5080 0.5120 0.5160 0.5199 0.5239 0.5279 0.5319 0.5359 0.5438 0.5478 0.5517 0.5557 0.5596 0.5636 0.5675 0.5714 0.5753 0.5832 0.5871 0.5910 0.5948 0.5987 0.6026 0.6064 0.6103 0.6141 0.6217 0.6255 0.6293 0.6331 0.6368 0.6406 0.6443 0.6480 0.6517 0.6591 0.6628 0.6664 0.6700 0.6736 0.6772 0.6808 0.6844 0.6879 0.6950 0.6985 0.7019 0.7054 0.7088 0.7123 0.7157 0.7190 0.7224 0.7291 0.7324 0.7357 0.7389 0.7422 0.7454 0.7486 0.7517 0.7549 0.7611 0.7642 0.7673 0.7704 0.7734 0.7764 0.7794 0.7823 0.7852 0.7910 0.7939 0.7967 0.7995 0.8023 0.8051 0.8078 0.8106 0.8133 0.8438 0.8461 0.8485 0.8508 0.8531 0.8554 0.8577 0.8599 0.8621 0.8665 0.8686 0.8708 0.8729 0.8749 0.8770 0.8790 0.8810 0.8830 0.8869 0.8888 0.8907 0.8925 0.8944 0.8962 0.8980 0.8997 0.9015 0.9049 0.9066 0.9082 0.9099 0.9115 0.9131 0.9147 0.9162 0.9177 0.9207 0.9222 0.9236 0.9251 0.9265 0.9279 0.9292 0.9306 0.9319 0.9345 0.9357 0.9370 0.9382 0.9394 0.9406 0.9418 0.9429 0.9441 0.9463 0.9474 0.9484 0.9495 0.9505 0.9515 0.9525 0.9535 0.9545 0.9564 0.9573 0.9582 0.9591 0.9599 0.9608 0.9616 0.9625 0.9633 0.9649 0.9656 0.9664 0.9671 0.9678 0.9686 0.9693 0.9699 0.9706 0.9719 0.9726 0.9732 0.9738 0.9744 0.9750 0.9756 0.9761 0.9767 0.9778 0.9783 0.9788 0.9793 0.9798 0.9803 0.9808 0.9812 0.9817 0.9826 0.9830 0.9834 0.9838 0.9842 0.9846 0.9850 0.9854 0.9857 0.9864 0.9868 0.9871 0.9875 0.9878 0.9881 0.9884 0.9887 0.9890 0.9896 0.9898 0.9901 0.9904 0.9906 0.9909 0.9911 0.9913 0.9916 0.9920 0.9922 0.9925 0.9927 0.9929 0.9931 0.9932 0.9934 0.9936 0.9940 0.9941 0.9943 0.9945 0.9946 0.9948 0.9949 0.9951 0.9952 0.9955 0.9956 0.9957 0.9959 0.9960 0.9961 0.9962 0.9963 0.9964 0.9966 0.9967 0.9968 0.9969 0.9970 0.9971 0.9972 0.9973 0.9974 0.9975 0.9976 0.9977 0.9977 0.9978 0.9979 0.9979 0.9980 0.9981 0.9982 0.9982 0.9983 0.9984 0.9984 0.9985 0.9985 0.9986 0.9986 0.9987 0.9987 0.9988 0.9988 0.9989 0.9989 0.9989 0.9990 0.9990 0.9991 0.9991 0.9991 0.9992 0.9992 0.9992 0.9992 0.9993 0.9993 0.9993 0.9994 0.9994 0.9994 0.9994 0.9994 0.9995 0.9995 0.9995 0.9995 0.9995 0.9996 0.9996 0.9996 0.9996 0.9996 0.9996 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9998