A random variable X has distribution function where ???? and m are positive constants. (i) Identify the
Question:
A random variable X has distribution function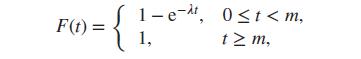
where ???? and m are positive constants.
(i) Identify the point(s) at which F has jumps.
(ii) Find the density function associated with the continuous part of this distribution.
(iii) Show that the expectation of X is
11. An insurance contract with deductible amount a and retention level b (with 0
b) entails the following agreement: Let Y be the size of the loss incurred to the insured. If Y ≤
a, the customer pays the full amount of this loss, while if a
b, the customer is responsible for the amount a and the company pays the difference Y −
a. Finally, for Y >
b, the company pays the amount b −
a. The size of the customer’s loss Y is a continuous random variable with distribution function FY and density fY .
(i) Verify that the distribution function F of the amount X that the company pays for a claim is given by the expression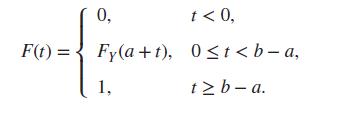
(ii) Show that the density, f2, for the continuous part of F is f2(x) = f (a + x), 0
a, while the probability function associated with the discrete part of F is given by f1(0) = FY (a), f1(b −
a) = 1 − FY (b).
(iii) Prove that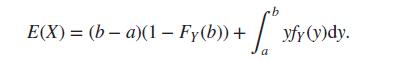
(iv) Give numerical answers to Parts (ii) and (iii) when Y has the density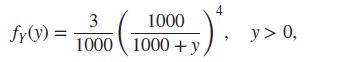
while a and b can be determined by knowing that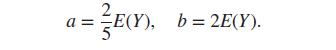
Step by Step Answer:

Introduction To Probability Volume 2
ISBN: 9781118123331
1st Edition
Authors: Narayanaswamy Balakrishnan, Markos V. Koutras, Konstadinos G. Politis






