Consider the sample space S 0, 1 with a probability measure that is uniform on this space, i e , Define the sequence X n , n 1, 2, as follows Also, define the random variable X on this sample space as follows Show that X n a s X P( a, b ) b a, for all 0 a b 1 ...

Define the set A as follows s S lim X s Xs n0 A s We need to prove that PA 1 Lets first fi ...

Consider the sample space S = [0, 1] with a probability measure that is uniform on this

Question:

Consider the sample space S = [0, 1] with a probability measure that is uniform on this space, i.e., P([a, b])=b-a, for all 0 < a < b < 1.

Define the sequence {X_n, n = 1, 2,⋯} as follows: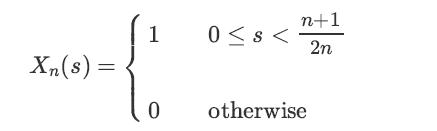 Xn(s) = { 1 0 0 < s < n+1 2n otherwise

Also, define the random variable X on this sample space as follows: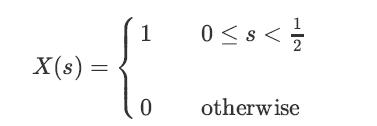 X(s) = 1 0 08 < = /2 otherwise

Show that X_n ^a.s.→ X.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Introduction To Probability Statistics And Random Processes

ISBN: 9780990637202

1st Edition

Authors: Hossein Pishro-Nik

See More Books

Question Posted: Oct 27, 2023 02:35 AM

See More Questions

Rewrite the following one line statement as another one line statement, but without x = a; X= Note: You may assume that the first line compiles correctly without warning.
Consider the sample space S = {copper, sodium, nitrogen, potassium, uranium, oxygen, zinc}, and the events A = {copper, sodium, zinc}, B = {sodium, nitrogen, potassium}, C = {oxygen}. List the...
Consider the experiment depicted by the Venn diagram, with the sample space S containing five sample points. The sample points are assigned the following probabilities: P(E1 = .20, P(E2) = .30, P(E3)...
Dominic and Magalie have been married for five years and have thes children, aged four, seven and nine. Dominic and Magale are diverong and Magalie has been ordered to pay child support, until the...
Bonnie purchased a new business asset (five-year property) on March 10, 2007, at a cost of $20,000. She also purchased a new business asset (seven-year property) on November 20, 2007, at a cost of...
What is corporate risk management? Why is it important to all firms? Assume you have just been hired as a financial analyst by Tennessee Sunshine Inc., a midsized Tennessee company that specializes...
LO4 How is gross income different from income?
Alaska Airlines and United Continental are both passenger airline companies. Although they use similar assets to conduct their businesses, the estimated lives they use to depreciate their assets...
A firm is borrowing $1 million to expand its operations. The annual interest on the loan is 13% and the loan will be repaid in quarterly installments over the next for ten years. What will the...
Find two sequences of random variables {X n , n = 1, 2,} and {Y n , n = 1, 2,} such that but X n + Y n does not converge in distribution to X +Y. d Xn X, and d Y Y, n
We perform the following random experiment. We put n 10 blue balls and n red balls in a bag. We pick 10 balls at random (without replacement) from the bag. Let X n be the number of blue balls. We...
Return to Review Question 7.2 and prepare a statement of financial position as at 30 June 2012. Review Question 7.2 From the following trial balance of G. Foot after his first years trading, you are...
Harry and Sally went to a large hardware store and told the salesperson they wanted the cheapest rotating clothesline in stock, provided it would bear a heavy load of washing. The salesperson assured...
do you agree wih this approach to dismantling the toxic culture? explain
Movies When randomly selecting a speaking character in a movie, the probability of getting a female is 0.331 (based on data from "Inequality in 1200 Popular Films," by Smith, et al., Annenberg...
Steve Reese is a well-known interior designer in Fort Worth, Texas. He wants to start his own business and convinces Rob O'Donnell, a local merchant, to contribute the capital to form a partnership....
Exercise 6-10A (Algo) Double-declining-balance and units-of-production depreciation: gain or loss on disposal LO 6-3, 6-4, 6-5 Exact Photo Service purchased a new color printer at the beginning of...
Identify the major events that occur during skeletal muscle fiber contraction.
The cash records of Holly Company show the following four situations. 1. The June 30 bank reconciliation indicated that deposits in transit total $720. During July, the general ledger account Cash...
AgriChem, Inc., has introduced an innovative new producta combination fertilizer, weed killer, and insecticide that makes it much easier for soybean farmers to produce a profitable crop. The product...
Review the Dell case at the beginning of the chapter and then discuss the compet i tive advantages that Barnes & Noble would have over a small bookshop. What advantages does a small bookshop have?
Give two examples of service firms that work with other channel specialists to sell their products to final consumers. What marketing functions is the specialist providing in each case?
Ron (78) is single and retired many years ago. during the tax year, he received a federally taxable private pension distribution of $19563. His Ohio income tax base is $55194. What is the amount of...
On January 1, 2020, Victory Co. acquired 60% of the shares of Sauce Ltd. by issuing shares valued at $1,500,000. On this date, Sauce Ltd.'s building and machinery had remaining useful lives of 10...
Anderson Co. issued a $59,335, 60-day, discounted note to National Bank. The discount rate is 7%. At maturity, assuming a 360-day year, the borrower will pay a.$60,027 b.$59,335 c.$55,182 d.$58,643

Consider the sample space S = [0, 1] with a probability measure that is uniform on this

Question:

P([a, b])=b-a, for all 0 < a < b < 1.

Step by Step Answer:

Define the set A as follows s S lim X s Xs n0 A s We need to prove that PA 1 Lets first fi...View the full answer

Introduction To Probability Statistics And Random Processes

Students also viewed these Business questions