Consider the set of points in the set C: Suppose that we pick a point (X, Y)
Question:
Consider the set of points in the set C: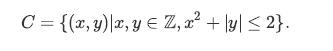
Suppose that we pick a point (X, Y) from this set completely at random. Thus, each point has a probability of 1/11 of being chosen.
a. Find the joint and marginal PMFs of X and Y.
b. Find the conditional PMF of X given Y = 1.
c. Are X and Y independent?
d. Find E[XY2].
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
a To find the joint and marginal PMFs of X and Y we need to consider all possible pairs of values x ...View the full answer
Answered By
Mustafa olang
Please accept my enthusiastic application to solutionInn. I would love the opportunity to be a hardworking, passionate member of your tutoring program. As soon as I read the description of the program, I knew I was a well-qualified candidate for the position.
I have extensive tutoring experience in a variety of fields. I have tutored in English as well as Calculus. I have helped students learn to analyze literature, write essays, understand historical events, and graph parabolas. Your program requires that tutors be able to assist students in multiple subjects, and my experience would allow me to do just that.
You also state in your job posting that you require tutors that can work with students of all ages. As a summer camp counselor, I have experience working with preschool and kindergarten-age students. I have also tutored middle school students in reading, as well as college and high school students. Through these tutoring and counseling positions, I have learned how to best teach each age group. For example, I created songs to teach my three-year-old campers the camp rules, but I gave my college student daily quizzes to help her prepare for exams.
I am passionate about helping students improve in all academic subjects. I still remember my excitement when my calculus student received her first “A” on a quiz! I am confident that my passion and experience are the qualities you are looking for at solutionInn. Thank you so much for your time and consideration.
2+ Reviews
10+ Question Solved
Related Book For 
Introduction To Probability Statistics And Random Processes
ISBN: 9780990637202
1st Edition
Authors: Hossein Pishro-Nik
Question Posted:
