Let FX be the distribution function and fX be the density function of a variable X for which we know that P(X ≥

a) = 1, where a ∈ ℝ is a given constant. We define the function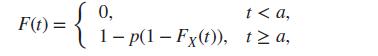

where 0 (i) Verify that F is the distribution function of a random variable Y, which is neither (purely) discrete nor continuous, and which takes the value a with probability 1 − p. Express the density function of Y in terms of fX.
(ii) Derive an expression for the expected value of Y in terms of E(X).
(iii) Write F in the form F = (1 − p)F1 + pF2, where F1 and F2 are suitable distribution functions of two random variables.

0, F(t) = t