Let X 2 , X 3 , X 4 , be a sequence of random variables such that Show that X n converges in distribution to X 1 Fx, (x) en(x 1) 1 en (2 1) 0 x 0 otherwise...

To show that the sequence of random variables X2 X3 X4 converges in distribution to X 1 we need to d ...

Let X 2 , X 3 , X 4 , be a sequence of random variables

Question:

Let X₂, X₃, X₄, ⋯ be a sequence of random variables such that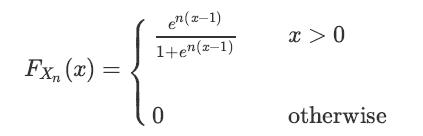 Fx, (x) = en(x-1) 1+en (2-1) 0 x>0 otherwise

Show that X_n converges in distribution to X = 1.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Introduction To Probability Statistics And Random Processes

ISBN: 9780990637202

1st Edition

Authors: Hossein Pishro-Nik

See More Books

Question Posted: Oct 27, 2023 02:35 AM

See More Questions

In Exercises use LHpitals Rule to evaluate the limit. (In x) lim x1 x 1
In Exercises, use the properties of logarithms to expand the logarithmic expression. In X 1
1. Resolve Class C 192.168.23.36 /27 2. Design DMZ minimumof 4 servers assigning an IP addressfor all devices 3. List and explain 4 primary servers that will be in the DMZ 4. Resolve Class C 192.168...
What exactly does it mean to say that the goal is to maximize shareholder wealth?
You have just graduated from the MBA program of a large university, and one of your favorite courses was "Today's Entrepreneurs." In fact, you enjoyed it so much you have decided you want to "be your...
LO2 Why is a tax on real property used more often than a tax on personal property?
The trial balance for Pioneer Advertising is shown in Illustration. Instead of the adjusting entries shown in the textbook at October 31, assume the following adjustment data. 1. Supplies on hand at...
Question 2 (36 marks) The accounting manager has requested you to calculate the throughput time, delivery cycle time, and MCE. The following average times have been recorded for the last four months:...
Let X 2 , X 3 , X 4 , be a sequence of random variables such that Show that X n converges in distribution to Uniform(0, 1). Fxn(x) = = enx + xen n+. enz + (+ ) en n enx ten - (+) en enx + 0x 1 x > 1
Let X 1 , X 2 , X 3 , be a sequence of random variable such that where > 0 is a constant. Show that X n converges in distribution to Poisson(). (MA). n Xn Binomialn, for n E N, n>d,
The box slides down the path described by the equation y = (0.05x) m, where x is in meters. If the box has x components of velocity and acceleration of v x , = -3 m/s and a x = -1.5 m/s at x = 5 m,...
Simplify. 32-6 3-6
1. (5 pts) Given y[n]= 2y[n-1] and y[0]=2, Write MATLAB code to calculate and plot y for 0
F ( t ) = t 4 + 1 8 t 2 + 8 1 2 , g ( t ) = ( t + 3 ) / 3 ; find ( f o g ) ( 9 )
How did they calculate allocated cost FLIGHT A FLIGHT 350 615 FLIGHT 3 1 Go GALS 20 G EXISTING SCHEME, DETERMINE THE OVE OR FLIGHTS A, B, AND C. 2 ED AT 7.00 PER K1.00 OF PILOT SALAF TOTAL NON-SALARY...
High Tech ManufacturingInc., incurred total indirect manufacturing labor costs of $540,000. The company is labor-intensive. Total labor hours during the period were 5,000. Using qualitativeanalysis,...
Describe the process of aging as it contributes to the stiffening of fibrous, cartilaginous and synovial joints.
Synthesize the products by drawing out reagents and intermediates along the way. `N H. OH HO HO
Explain the total cost approach and why it may cause conflicts in some firms. Give examples of how conflicts might occur between different departments.
Discuss why economies of scale in transportation might encourage a producer to include a regional merchant wholesaler in the channel of distribution for its consumer product.
Discuss some of the ways that air transportation can change other aspects of a Place system.
How should a material unusual or infrequent gain or loss be disclosed in the financial statements?
Refer to Figure 4-20. All else equal, a major paper manufacturer filing for bankruptcy and shutting down as a result of an IRS tax evasion investigation would cause a move from
Coronado Corporation purchased a truck at the beginning of 2020 for $56,000. The truck is estimated to have a salvage value of $2,240 and a useful life of 179,200 miles. It was driven 25,760 miles in...

Let X 2 , X 3 , X 4 , be a sequence of random variables

Question:

Fx₁, (x) = en(x-1) 1+en (2-1) 0 x>0 otherwise

Step by Step Answer:

To show that the sequence of random variables X2 X3 X4 converges in distribution to X 1 we need to d...View the full answer

Introduction To Probability Statistics And Random Processes

Students also viewed these Business questions