Let X be a random variable that has the geometric distribution with parameter p

(0 < p < 1), and let f be the probability function of X.

(i) Verify that f satisfies the recursive relationship f (x) = (1 − p)f (x − 1), x = 2, 3,…, with the initial condition f (1) = p.

(ii) Verify that f (x) < f (x − 1) for any x = 2, 3,…

(iii) Show that the rth factorial moment of X

????(r) = E[X(X − 1)(X − 2) · · · (X − r + 1)]

is given by the formula

????(r) = r!

(1 − p)r−1 pr , r ≥ 1.

(Hint: For Part (iii), differentiate r times the geometric series 1 + t + t2 + · · · + tn + · · · = 1 1 − t , for |t| < 1, and check that the following identity ensues: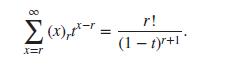

Then use this identity to complete your derivation.)