Let Xn be the number of successes in n independent Bernoulli trials, each with a success probability
Question:
Let Xn be the number of successes in n independent Bernoulli trials, each with a success probability p, and![]()
(i) Using the law of total probability and the partition {B1, B2} with B1 = {X1 = 0}, and B2 = {X1 = 1}, prove that the following recursion holds:
an = (1 − p)an−1 + p(1 − an−1), n = 2, 3,…
(ii) Show by induction that the numbers an, n = 1, 2,…, are given by an = 1 2 [1 + (1 − 2p)n], n = 1, 2,…
(iii) Using the result from (ii), deduce the combinatorial identity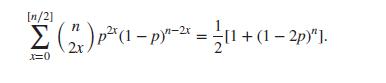
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Introduction To Probability Volume 2
ISBN: 9781118123331
1st Edition
Authors: Narayanaswamy Balakrishnan, Markos V. Koutras, Konstadinos G. Politis
Question Posted:






