Let {X(t), t ∈ R} and {Y (t), t ∈ R} be two independent random processes. Let Z(t) be defined as

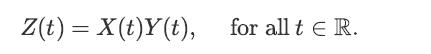
Prove the following statements:

a. μ_Z(t) = μ_X(t)μ_Y (t), for all t ∈ R.

b. R_Z(t₁, t₂) = R_X(t₁, t₂)R_Y (t₁, t₂), for all t ∈ R.

c. If X(t) and Y (t) are WSS, then they are jointly WSS.

d. If X(t) and Y (t) are WSS, then Z(t) is also WSS.

e. If X(t) and Y (t) are WSS, then X(t) and Z(t) are jointly WSS.

Transcribed Image Text:

Z(t) = X(t)Y(t), for all t € R.