The total sum of squares is given by (sum_{i=1}^{k} sum_{j=1}^{r}left(y_{i j}-bar{y} ight)^{2}) where the overall mean (bar{y}=sum_{i=1}^{k}

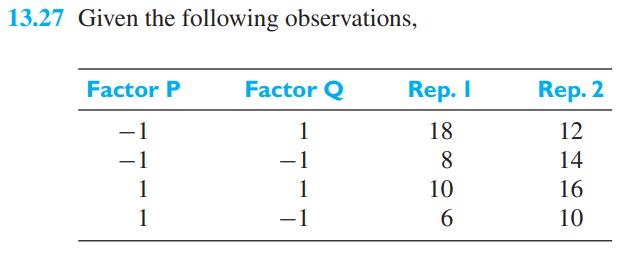
The total sum of squares is given by \(\sum_{i=1}^{k} \sum_{j=1}^{r}\left(y_{i j}-\bar{y}\right)^{2}\) where the overall mean \(\bar{y}=\sum_{i=1}^{k} \sum_{j=1}^{r}\left(y_{i j} / n\right)\). With reference to Exercise 13.27, show that the total sum of squares can be expressed as the sum of squares due to each of the treatment SSA, \(S S B\), and \(S S A B\) plus the error of the sum of squares.

This decomposition is the basis for the analysis of variance and it is summarized in the first column of the ANOVA table.

Sum of squares for any treatment in a \(2^{2}\) design is (estimated effect) \({ }^{2} \times r\). The error of the sum of squares is \(\left.\sum_{i=1}^{k} \sum_{j=1}^{r}\left(y_{i j}-\bar{y}_{i}\right)^{2}\right]\)

Data From Exercise 13.27

Transcribed Image Text:

13.27 Given the following observations, Factor P Factor Q Rep. I Rep. 2 1 18 12 8 14 1 1 10 16 1 -1 6 10