Two gamblers, call them Gambler A and Gambler B, play repeatedly. In each round, A wins 1
Question:
Two gamblers, call them Gambler A and Gambler B, play repeatedly. In each round, A wins 1 dollar with probability p or loses 1 dollar with probability q = 1 −p (thus, equivalently, in each round B wins 1 dollar with probability q = 1 −p and loses 1 dollar with probability p). We assume different rounds are independent. Suppose that initially A has i dollars and B has N −i dollars. The game ends when one of the gamblers runs out of money (in which case the other gambler will have N dollars). Our goal is to find pi, the probability that A wins the game given that he has initially i dollars.
a. Define a Markov chain as follows: The chain is in state i if the Gambler A has i dollars. Here, the state space is S = {0, 1,⋯,N}. Draw the state transition diagram of this chain.
b. Let ai be the probability of absorption to state N (the probability that A wins) given that X0 = i. Show that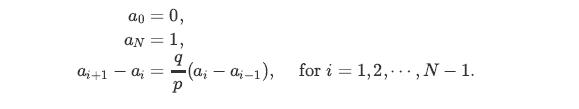
c. Show that![2 i-17 9 = [ + + ( ) + + + ( ) ^ ] - 9 P P P a, for i=1,2,..., N.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1698/3/9/3/888653b6f209d9e31698393883997.jpg)
d. Find ai for any i ∈ {0, 1, 2,⋯,N}. Consider two cases: p = 1/2 and p ≠ 1/2.
Step by Step Answer:

Introduction To Probability Statistics And Random Processes
ISBN: 9780990637202
1st Edition
Authors: Hossein Pishro-Nik




