When we use the Inverse Transformation Method, we need a simple form of the cdf F(x) that allows direct computation of X = F^-1(U). When F(x) doesn't have a simple form but the pdf f(x) is available, random variables with density f(x) can be generated by the rejection method. Suppose you have a method for generating a random variable having density function g(x). Now, assume you want to generate a random variable having density function f(x). Let c be a constant such that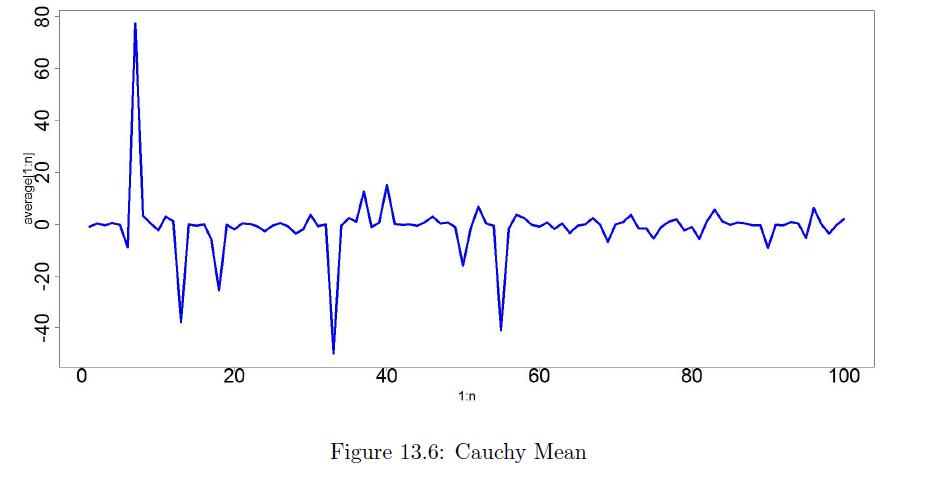

Show that the following method generates a random variable with density function f(x).

- Generate Y having density g.

- Generate a random number U from Uniform (0; 1).

- If U ≤ f(Y )/cg(Y ) , set X = Y. Otherwise, return to step 1.

80 average 1:n 60 40 20 0 -20 -40 0 20 pornog 40 1:n 60 Figure 13.6: Cauchy Mean 80 100