In 1843, Sir William Hamilton discovered an extension to complex numbers called quaternions. A quaternion is a 4-tuple \(a=\left(a_{0}, a_{1}, a_{2}, a_{3}ight)\) with the following operations:

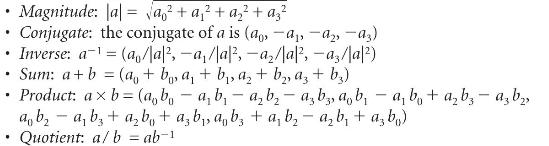
Create a data type Quaternion for quaternions and a test client that exercises all of your code. Quaternions extend the concept of rotation in three dimensions to four dimensions. They are used in computer graphics, control theory, signal processing, and orbital mechanics.

Magnitude: |a| = a + a + a + az . Conjugate: the conjugate of a is (ao, -a, -a, -az) Inverse: a = (a/la, -a/a, -a/a, -a3/a) Sum: a+b = (a + b, a + b, a + b, a3 + b) . Product: axb= (a, b, a, b-ab - a, b, a, b, a, b + ab3-a3b ab-ab+ ab + abab3 + ab-ab + ab) Quotient: a/b = ab-1 . . .