(a) Prove the following corollary to the variational principle: If (| gs ) = 0, then (H)...
Question:
(a) Prove the following corollary to the variational principle: If (Ψ|Ψgs) = 0, then (H) ≥ Efe, where is the energy of the first excited state. Comment: If we can find a trial function that is orthogonal to the exact ground state, we can get an upper bound on the first excited state. In general, it’s difficult to be sure that Ψ is orthogonal to Ψgs, since (presumably) we don’t know the latter. However, if the potential V(x) is an even function of x, then the ground state is likewise even, and hence any odd trial function will automatically meet the condition for the corollary.
(b) Find the best bound on the first excited state of the one-dimensional harmonic oscillator using the trial function
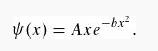
Step by Step Answer:

Introduction To Quantum Mechanics
ISBN: 9781107189638
3rd Edition
Authors: David J. Griffiths, Darrell F. Schroeter





