(a) Suppose you could find a solution (r 1 ,r 2 , ..., r z ) to the Schrdinger equation (Equation 5.37), for the

(a) Suppose you could find a solution Ψ (r₁,r₂, ..., r_z) to the Schrödinger equation (Equation 5.37), for the Hamiltonian in Equation 5.36. Describe how you would construct from it a completely symmetric function, and a completely antisymmetric function, which also satisfy the Schrödinger equation, with the same energy. What happens to the completely antisymmetric function if Ψ (r₁,r₂, ..., r_z) is symmetric in (say) its first two arguments (r₁ ↔  r₂)?
(b) By the same logic, show that a completely antisymmetric spin state for Z electrons is impossible, if Z > 2 (this generalizes Problem 5.10(a)).

Equation 5.36

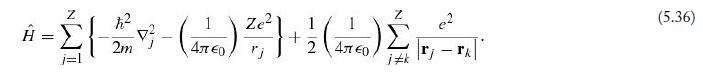
Equation 5.37

Problem 5.10(a)

(a) Prove it.

What does antisymmetry under 1 ↔ 2 tell you about the coefficients?

(5.36) 1x| = 507) (2207) 43-