Coherent states of the harmonic oscillator. Among the stationary states of the harmonic oscillator (Equation 2.68) only n = 0 hits the uncertainty limit (σ_x σ_p = ћ/2); in general, σ_x σ_p = (2n + 1)  ћ/2, as you found in Problem 2.12. But certain linear combinations (known as coherent states) also minimize the uncertainty product. They are (as it turns out) eigenfunctions of the lowering operator:

(the eigenvalue α can be any complex number).
(a) Calculate (x), (x²), (p), (p²) in the state |α>.
(b) Find σ_x and σ_p; show that σ_x σ_p = ћ/2.
(c) Like any other wave function, a coherent state can be expanded in terms of energy eigenstates:

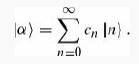
Show that the expansion coefficients are

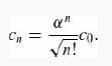
(d) Determine c₀ by normalizing |α>. 

(e) Now put in the time dependence:

and show that |α (t)} remains an eigenstate of α⇁ but the eigenvalue evolves in time:

So a coherent state stays coherent, and continues to minimize the uncertainty product.
(f) Based on your answers to (a), (b), and (e), find (x) and σ_x as functions of time. It helps if you write the complex number α as 

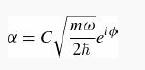
for real numbers C and ϕ. In a sense, coherent states behave quasi-classically.
(g) Is the ground state {|n = 0}) itself a coherent state? If so, what is the eigenvalue?

Problem 2.12

Find (x), (p), (x²),(p²) and (T), for the nth stationary state of the harmonic oscillator, using the method of Example 2.5. Check that the uncertainty principle is satisfied.

Equation 2.68

Transcribed Image Text:

a_ |α) = α|α)