Consider a free electron gas (Section 5.3.1) with unequal numbers of spin-up and spin-down particles (N +
Question:
Consider a free electron gas (Section 5.3.1) with unequal numbers of spin-up and spin-down particles (N+ and N- and respectively). Such a gas would have a net magnetization (magnetic dipole moment per unit volume)

where μB = eћ/2me is the Bohr magneton. (The minus sign is there, of course, because the charge of the electron is negative.)
(a) Assuming that the electrons occupy the lowest energy levels consistent with the number of particles in each spin orientation, find Etot. Check that your answer reduces to Equation 5.56 when N+ = N-.
(b) Show that for M/μB << ρ Ξ (N+ + N-)/V (which is to say, |N+ - N-| ,<< (N+ + N-)), the energy density is
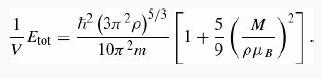
The energy is a minimum for M = 0, so the ground state will have zero magnetization. However, if the gas is placed in a magnetic field (or in the presence of interactions between the particles) it may be energetically favorable for the gas to magnetize. This is explored in Problems 5.33 and 5.34.
Equation 5.56
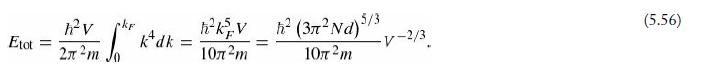
Step by Step Answer:

Introduction To Quantum Mechanics
ISBN: 9781107189638
3rd Edition
Authors: David J. Griffiths, Darrell F. Schroeter





