Consider a particle of mass m that is free to move in a one-dimensional region of length L that closes on itself (for instance, a bead that slides frictionlessly on a circular wire of circumference L, as in Problem 2.46).
(a) Show that the stationary states can be written in the form

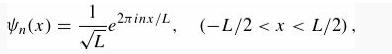
where n = 0, ±1, ±2, … , and the allowed energies are

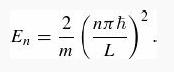
Notice that—with the exception of the ground state (n = 0) —these are all doubly degenerate.
(b) Now suppose we introduce the perturbation

where a << L. (This puts a little “dimple” in the potential at x = 0, as though we bent the wire slightly to make a “trap”.) Find the first-order correction to E_n, using Equation 7.33.
(c) What are the “good” linear combinations of Ψ_n and Ψ_-n, for this problem? use Eq. 7.27.) Show that with these states you get the first-order correction using Equation 7.9.
(d) Find a hermitian operator A that fits the requirements of the theorem, and show that the simultaneous eigenstates of H⁰ and A are precisely the ones you used in (c).

Transcribed Image Text:

1 Vn(x) = 2inx/L (L/2