Consider a perturbation to a two-level system with matrix elements where and are positive constants
Question:
Consider a perturbation to a two-level system with matrix elements
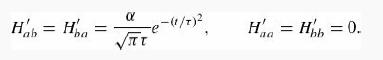
where τ and α are positive constants with the appropriate units.
(a) According to first-order perturbation theory, if the system starts off in the state Ca = 1, Cb = 0 at t = -∞, what is the probability that it will be found in the state b at t = ∞?
(b) In the limit that τ → 0, Hab = aδ(t). Compute the τ → 0 limit of your expression from part (a) and compare the result of Problem 11.4.
(c) Now consider the opposite extreme: ω0τ >> 1. What is the limit of your expression from part (a)? Comment: This is an example of the adiabatic theorem (Section 11.5.2).
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
a Using Equation 1121 The probability of a transition then is b In the limit 0 ...View the full answer
Answered By
Asim farooq
I have done MS finance and expertise in the field of Accounting, finance, cost accounting, security analysis and portfolio management and management, MS office is at my fingertips, I want my client to take advantage of my practical knowledge. I have been mentoring my client on a freelancer website from last two years, Currently I am working in Telecom company as a financial analyst and before that working as an accountant with Pepsi for one year. I also join a nonprofit organization as a finance assistant to my job duties are making payment to client after tax calculation, I have started my professional career from teaching I was teaching to a master's level student for two years in the evening.
My Expert Service
Financial accounting, Financial management, Cost accounting, Human resource management, Business communication and report writing. Financial accounting : • Journal entries • Financial statements including balance sheet, Profit & Loss account, Cash flow statement • Adjustment entries • Ratio analysis • Accounting concepts • Single entry accounting • Double entry accounting • Bills of exchange • Bank reconciliation statements Cost accounting : • Budgeting • Job order costing • Process costing • Cost of goods sold Financial management : • Capital budgeting • Net Present Value (NPV) • Internal Rate of Return (IRR) • Payback period • Discounted cash flows • Financial analysis • Capital assets pricing model • Simple interest, Compound interest & annuities
65+ Reviews
86+ Question Solved
Related Book For 
Introduction To Quantum Mechanics
ISBN: 9781107189638
3rd Edition
Authors: David J. Griffiths, Darrell F. Schroeter
Question Posted:
