Consider the potential where a is a positive constant, and sech stands for the hyperbolic secant. (a)
Question:
Consider the potential
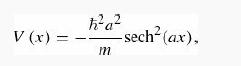 where a is a positive constant, and “sech” stands for the hyperbolic secant.
where a is a positive constant, and “sech” stands for the hyperbolic secant.
(a) Graph this potential.
(b) Check that this potential has the ground state
![]() and find its energy. Normalize Ψ0, and sketch its graph.
and find its energy. Normalize Ψ0, and sketch its graph.
(c) Show that the function
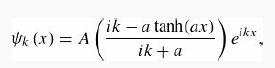
(where ![]() as usual) solves the Schrödinger equation for any(positive) energy E. Since tanh z → -1 as z → -
as usual) solves the Schrödinger equation for any(positive) energy E. Since tanh z → -1 as z → - ![]() ,
,
![]()
for large negative x.
This represents, then, a wave coming in from the left with no accompanying reflected wave (i.e. no term exp (-ikx)). What is the asymptotic form of Ψk (x) at large positive x? What are R and T, for this potential? This is a famous example of a reflectionless potential—every incident particle, regardless its energy, passes right through.
Step by Step Answer:

Introduction To Quantum Mechanics
ISBN: 9781107189638
3rd Edition
Authors: David J. Griffiths, Darrell F. Schroeter





