For any vector operator V one can define raising and lowering operators as (a) Using Equation 6.33, show that (b) Show that, if is

For any vector operator  V̂ one can define raising and lowering operators as

(a) Using Equation 6.33, show that

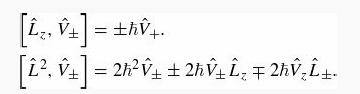(b) Show that, if Ψ is an eigenstate of L̂² and L̂_z with eigenvalues ℓ(ℓ+1) ћ² and ℓћ respectively, then either V̂+Ψ is zero or V̂+Ψ is also an eigenstate of  L̂² and L̂_z with eigenvalues (ℓ+1) (ℓ+2) ћ² and (ℓ+1) ћ respectively. This means that, acting on a state with maximal mℓ = ℓ, the operator V̂+ either “raises” both the ℓ and m values by 1 or destroys the state.

vt = V ivy.