In Section 5.3.1 we put the electrons in a box with impenetrable walls. The same results can be obtained using periodic boundary conditions. We still imagine the electrons to be confined to a box with sides of length l_x, l_y, and l_z but instead of requiring the wave function to vanish on each wall, we require it to take the same value on opposite walls:

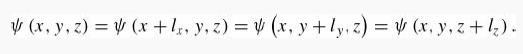
In this case we can represent the wave functions as traveling waves,

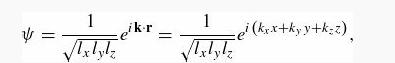
rather than as standing waves (Equation 5.49). Periodic boundary conditions— while certainly not physical—are often easier to work with (to describe something like electrical current a basis of traveling waves is more natural than a basis of standing waves) and if you are computing bulk properties of a material it shouldn’t matter which you use.
(a) Show that with periodic boundary conditions the wave vector satisfies

where each n is an integer (not necessarily positive). What is the k-space volume occupied by each block on the grid (corresponding to Equation 5.51)?

(b) Compute k_F, E_F, and E_tot for the free electron gas with periodic boundary conditions. What compensates for the larger volume occupied by each k-space block (part (a)) to make these all come out the same as in Section 5.3.1?

Transcribed Image Text:

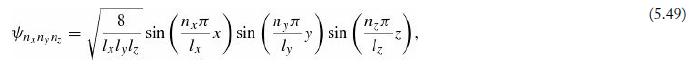
(x, y, z) = (x+l, y, z)=(x, y +ly, z)=(x, y, z+1₂).