In this problem we explore some of the more useful theorems (stated without proof) involving Hermite polynomials.
(a) The Rodrigues formula says that

Use it to derive H₃ and H₄ .
(b) The following recursion relation gives you H_n+1 in terms of the two preceding Hermite polynomials:

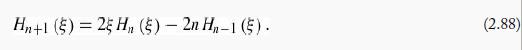
Use it, together with your answer in (a), to obtain H₅ and H₆.
(c) If you differentiate an nth-order polynomial, you get a polynomial of order (n-1) . For the Hermite polynomials, in fact,

Check this, by differentiating H₅ and H₆.

(d)  H_n (ξ) is the nth z-derivative, at  z = 0, of the generating function exp (-z² + 2zξ); or, to put it another way, it is the coefficient of z^ћ/n! in the Taylor series expansion for this function:

Use this to obtain H₁ , H₂ and H₃.

Transcribed Image Text:

H₁, (§) = (-1)" e² d (4) * e²². (2.87)