In this problem we will recover the results Section 11.2.1 directly from the Hamiltonian for a charged particle in an electromagnetic field (Equation 4.188). An electromagnetic wave can be described by the potentials

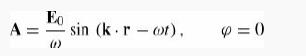
where in order to satisfy Maxwell’s equations, the wave must be transverse (E₀ . k = 0) and of course travel at the speed of light (ω = c|k|).
(a) Find the electric and magnetic fields for this plane wave.
(b) The Hamiltonian may be written as H⁰ + H' where H⁰ is the Hamiltonian in the absence of the electromagnetic wave and H' is the perturbation. Show that the perturbation is given by

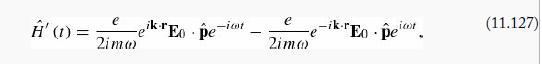
plus a term proportional to E²₀ that we will ignore.
(c) In the dipole approximation we set e^ik.r ≈ 1. With the electromagnetic wave polarized along the z direction, show that the matrix element for absorption is then

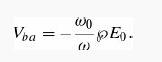Compare Equation 11.41. They’re not exactly the same; would the difference effect our calculations in Section 11.2.3 or 11.3? Why or why not?

A = Eo sin (k root), 9=0