Its obvious that the trace of a diagonal matrix is the sum of its eigenvalues, and its
Question:
It’s obvious that the trace of a diagonal matrix is the sum of its eigenvalues, and its determinant is their product (just look at Equation A.79). It follows (from Equations A.65 and A.68) that the same holds for any diagonalizable matrix. Prove that in fact
![]()
for any matrix. (The λ’s are the n solutions to the characteristic equation—in the case of multiple roots, there may be fewer linearly-independent eigenvectors than there are solutions, but we still count each λ as many times as it occurs.)
![]()
and use the result of Problem A.20.
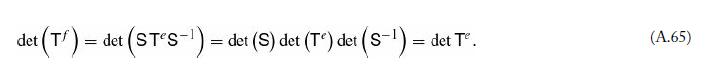
![]()

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Introduction To Quantum Mechanics
ISBN: 9781107189638
3rd Edition
Authors: David J. Griffiths, Darrell F. Schroeter
Question Posted:





