Suppose you’re given a two-level quantum system whose (time-independent) Hamiltonian H⁰ admits just two eigenstates, Ψ_a (with energy E_a), and Ψ_b (with energy E_b). They are orthogonal, normalized, and nondegenerate (assume E_a is the smaller of the two energies). Now we turn on a perturbation H', with the following matrix elements:

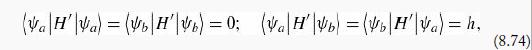
where h is some specified constant.
(a) Find the exact eigenvalues of the perturbed Hamiltonian.
(b) Estimate the energies of the perturbed system using second-order perturbation theory.
(c) Estimate the ground state energy of the perturbed system using the variational principle, with a trial function of the form

where ϕ is an adjustable parameter. Note: Writing the linear combination in this way is just a neat way to guarantee that Ψ is normalized.
(d) Compare your answers to (a), (b), and (c). Why is the variational principle so accurate, in this case?

Transcribed Image Text:

(Va|H|Va) = (b|H|V₂) = 0; (Va|H|Vb) = (v₁|H²|ya) = h, (8.74)