Prove Theorem 3.3 using the theorems of Borel and Cantelli. That is, let \(\left\{X_{n}ight\}_{n=1}^{\infty}\) be a sequence of random variables that converges completely to a random variable \(X\) as \(n ightarrow \infty\). Then prove that \(X_{n} \xrightarrow{\text { a.c. }} X\) as \(n ightarrow \infty\) using Theorems 2.17 and 2.18.

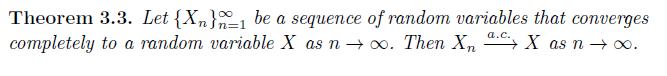
Transcribed Image Text:

Theorem 3.3. Let {X} be a sequence of random variables that converges completely to a random variable X as n o. Then Xn X as n. a.c.