Write a program in (mathrm{R}) that generates a sample of size (b) from a specified distribution (F_{n})
Question:
Write a program in \(\mathrm{R}\) that generates a sample of size \(b\) from a specified distribution \(F_{n}\) (specified below) that weakly converges to a distribution \(F\) as \(n ightarrow \infty\). Compute the Kolmogorov distance between \(F\) and the empirical distribution from the sample. Repeat this for \(n=5,10,25,50,100,500\), and 1000 with \(b=10,000\) for each of the cases given below. Discuss the behavior of the Kolmogorov distance and \(n\) becomes large in terms of the result of Theorem 4.7 (Pólya). Be sure to notice the specific assumptions that are a part of Theorem 4.7.
a. \(F_{n}\) corresponds to a \(\operatorname{Normal}\left(n^{-1}, 1+n^{-1}ight)\) distribution and \(F\) corresponds to a \(\operatorname{Normal}(0,1)\) distribution.
b. \(F_{n}\) corresponds to a \(\operatorname{Gamma}\left(1+n^{-1}, 1+n^{-1}ight)\) distribution and \(F\) corresponds to a \(\operatorname{Gamma}(1,1)\) distribution.
c. \(F_{n}\) corresponds to a \(\operatorname{Binomial}\left(n, n^{-1}ight)\) distribution and \(F\) corresponds to a POISson(1) distribution.
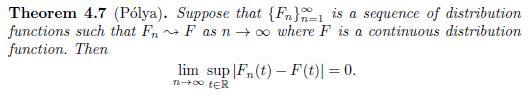
Step by Step Answer:






