A machine receives shocks at the times \(T_{1}, T_{2}, T_{3}, \ldots\) of a renewal process, and incurs damage at a level of \(D_{i}\) as a result of the \(i^{\text {th }}\) shock. The damage from each shock ebbs exponentially as time wears on. We shall suppose that the times \(T_{i+1}-T_{i}\) between shocks are independent of the damage levels \(D_{i}\), which are independent and identically distributed. Hence the total damage sustained by the machine up to time \(t\) can be written:

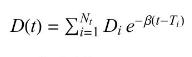
Write a simulation program that takes as parameters the probability distribution of the damages, the inter-renewal distribution, the constant \(\beta\), and a final time \(t\), and returns the cumulative damage level \(D(t)\) at time \(t\). Exercise your program in the case where the inter-renewal times have the exponential(2) distribution, \(\beta=.01\), the damage levels have the continuous uniform distribution on the interval \([0,1]\). By running the simulation many times, use the average damage level \(\bar{D}(t)\) in the simulated trials to estimate the expectation \(E[D(t)]\). Repeat for several different times \(t\) and generate a list plot in time to get an estimate of the function that maps \(t\) to \(E[D(t)]\).

Transcribed Image Text:

N D(t) = De B(1-T) De-B-T)