Adjacency matrices are not the only way of representing graphs. An adjacency list representation of a graph is a list, vertex-by-vertex, of the vertices that are adjacent to that vertex. For example, for the graph of Figure 1.4 one would have the adjacency list

\[ \begin{aligned} & v_{1}: v_{2}, v_{3}, v_{4} \\ & v_{2}: v_{1}, v_{4} \\ & v_{3}: v_{1} \end{aligned} \]

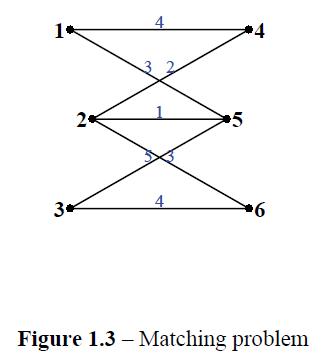
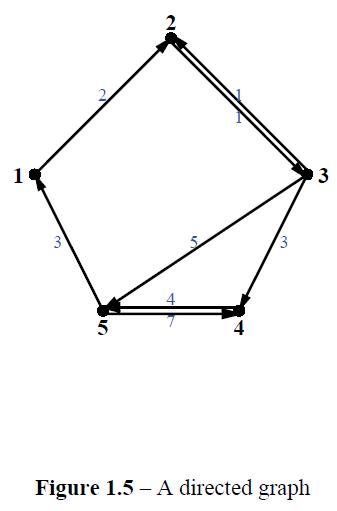
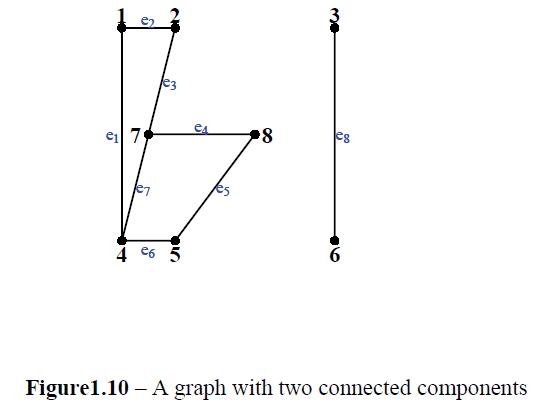
For graphs with many vertices and not very many edges, this representation can result in a substantial savings in the amount of information recorded. Write adjacency lists for the graphs of

(a) Figure 1.3;

(b) Figure 1.5;

(c) Figure 1.10.

Transcribed Image Text:

V3 4 Figure 1.4 - An undirected graph