Consider an (M / M / 1 / N) queue whose arrival and service rates are equal.
Question:
Consider an \(M / M / 1 / N\) queue whose arrival and service rates are equal. Suppose that customers who join the queue receive a reward \(R\) at the end of service, but pay at a rate of \(C\) per unit time while they are waiting. Find inequalities that characterize the optimal waiting room size \(N\) that maximizes the long-run expected profit per customer, per unit time:
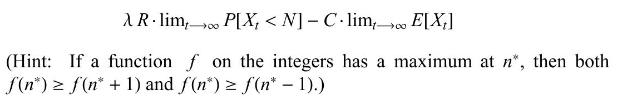
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Introduction To The Mathematics Of Operations Research With Mathematica
ISBN: 9781574446128
1st Edition
Authors: Kevin J Hastings
Question Posted:





