Let (left(X_{n} ight)) be a Markov chain with the transition matrix below. Show that the constant function
Question:
Let \(\left(X_{n}\right)\) be a Markov chain with the transition matrix below. Show that the constant function \(f=2\) is excessive (i.e., \(f \geqslant T \cdot f\) ). More generally, show that for an arbitrary Markov chain with finite state space, the constant function \(f=c\) is excessive.
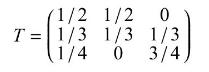
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Introduction To The Mathematics Of Operations Research With Mathematica
ISBN: 9781574446128
1st Edition
Authors: Kevin J Hastings
Question Posted:





