Let ( left(X n ight) ) be a two state Markov chain over which we have a degree of control, in the sense that the transition matrix is where ( varepsilon ) may be chosen from ( 1, 1 ) If we receive a reward of ( $ 2 ) when state 1 is occupied, and ( $ 1 ) when state 2 is occupied, and there is a dis...

The Answer is in the image, click to view ...

Let (left(X_{n} ight)) be a two-state Markov chain over which we have a degree of control, in

Question:

Let $\left(X_{n}\right)$ be a two-state Markov chain over which we have a degree of control, in the sense that the transition matrix is

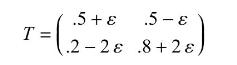
image text in transcribed

where $\varepsilon$ may be chosen from $[-.1, .1]$. If we receive a reward of $\$ 2$ when state 1 is occupied, and $\$ 1$ when state 2 is occupied, and there is a discount factor $\alpha=.9$, find $\varepsilon$ to maximize the expected total discounted reward starting at state 1 .

Fantastic news! We've Found the answer you've been seeking!