Suppose, in the optimal stopping problem, that there is a discount factor of \(\alpha \in(0,1)\) per period. That is, the reward collected when the game is stopped at time \(S\) is only \(\alpha^{S} f\left(X_{S}\right)\) in present-day terms.

(a) Use a dynamic programming argument to show that the optimal value function satisfies

where \(T\) is the transition matrix of the Markov chain.

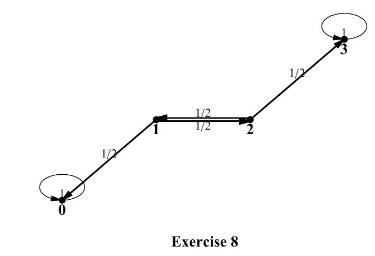
(b) Let us presume that it is still true that the optimal stopping time is the time at which the chain first enters the set \(A^{*}=\{i \in E: f(i)=V(i)\}\). Find the optimal stopping time for the chain whose transition diagram is below, if the reward function is \(f(i)=i\), and the discount factor is \(\alpha=.5\).

Transcribed Image Text:

V(i) = max {f(i), a T V(i)},