Problem 3.27 consists of an irreversible process in which an ideal gas with constant heat capacity was compressed in a piston–cylinder assembly. As part of this problem, you were asked to calculate Dssys for this process. Entropy change is defi ned for a reversible process as: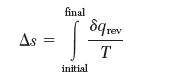

Since entropy is a property, the change in entropy depends only on the fi nal and initial states of the system, not on the path the system went through for a particular process. Therefore, we can pick any reversible path we want, as long as it takes us from the initial state to the final state. Calculate Δssys for the process depicted in Problem 3.27, using each of the following paths:

(a) a reversible, adiabatic compression, followed by a reversible, isothermal expansion (two of the four steps in the Carnot cycle)

(b) a reversible, isobaric heating followed by a reversible, isothermal compression

(c) a reversible, isochoric (constant-volume) heating followed by a reversible, isothermal compression

Problem 3.27

Consider the piston–cylinder assembly shown at the top of page. It is well insulated and initially contains two 5000-kg blocks at rest on the 0.05-m2 piston. The initial temperature is 500 K.
The ambient pressure is 5 bar. One mol of an ideal gas is contained in the cylinder. This gas is compressed in a process in which another 5000-kg block is added. The heat capacity of the gas at constant volume can be taken to have a constant value of (5/2) R, where R is the gas constant.

Transcribed Image Text:

As = final J initial 89 rev T